Stockage dense vs creux des matrices en FEM - Étude de cas sur une fondation d'éolienne
En ingénierie des structures, les modèles éléments finis (FEM) utilisent des matrices pour représenter la raideur du système et résoudre les déplacements. Chaque ligne (et colonne) d'une matrice correspond à un degré de liberté (DDL) de la structure. Lorsqu'on raffine le maillage, le nombre de DDL augmente, et la taille de la matrice de raideur croît au carré de ce nombre.
Ces matrices sont naturellement creuses (principalement composées de zéros en raison de la connectivité locale des éléments), mais les ingénieurs doivent choisir comment les stocker. Le stockage dense conserve naïvement toutes les entrées (y compris les zéros), tandis que le stockage creux les compresse. Ce choix impacte fortement la mémoire et les performances.
Pourquoi utiliser un stockage creux ?
Pour être honnête, je n'ai commencé à m'intéresser au stockage creux des matrices qu'après avoir atteint les limites de mon ordinateur en développant ma propre bibliothèque FEM.
Pour des structures courantes de génie civil modélisées avec des éléments poutres, la mémoire n'était pas un problème, et mon implémentation assemblait simplement la matrice complète. Cela fonctionnait très bien.
Mais quand je suis passé à des éléments volumiques pour mieux représenter des systèmes continus, la taille de la matrice de raideur a explosé.
En testant plusieurs modèles de taille moyenne, avec environ 10 000 nœuds, mon ordinateur saturait en mémoire et plantait. Après inspection, j'ai découvert que la matrice de raideur devenait gigantesque très rapidement.
Je me suis demandé comment c'était possible. Je savais que des logiciels commerciaux comme ANSYS pouvaient résoudre des modèles avec des centaines de milliers de nœuds sur la même machine.
La différence ? Le stockage creux.
La plupart des valeurs dans la matrice de raideur étaient des zéros « inutiles ». Le stockage creux élimine ces zéros et ne conserve que les valeurs non nulles et leurs indices.
Après avoir mis à jour mon solveur pour gérer les matrices creuses, ma bibliothèque FEM pouvait stocker des modèles avec des centaines de milliers de nœuds en mémoire, tout comme les logiciels commerciaux.
Quelle mémoire est nécessaire pour stocker la matrice de raideur ?
Estimons les besoins en mémoire pour stocker la matrice de raideur aux formats dense et creux.
Stockage dense
Dans une matrice dense, on stocke chaque entrée. Pour n DDL, on a une matrice n x n, soit n² valeurs flottantes. En stockant chaque valeur en double précision (8 octets), on a :
memoire = n * n * 8
Par exemple, un modèle avec 106 000 DDL nécessitait 83,90 Go de mémoire.
Stockage creux
Comme la plupart des coefficients de la matrice de raideur sont nuls, on peut stocker uniquement les coefficients non nuls, accompagnés de leurs indices de ligne et de colonne. En supposant que chaque élément non nul nécessite deux entiers de 4 octets et un flottant de 8 octets, la mémoire requise par élément non nul est :
mémoire = 2 * 4 bytes + 1 * 8 bytes = 16 bytes
Même si chaque élément stocké en format creux occupe plus d'octets qu'un élément en format dense (en raison de la surcharge liée à chaque valeur non nulle), le nombre de zéros est, dans la plupart des cas, plusieurs ordres de grandeur plus élevé, ce qui rend le stockage creux bien plus efficace.
Pour le même exemple avec 106 000 degrés de liberté, le stockage creux n'a requis que 40 Mo.
Fondation d'éolienne onshore - matrice de raideur
Appliquons maintenant ces concepts à un exemple réel de fondation d'éolienne terrestre.
Nous avons modélisé la fondation de l'éolienne à l'aide d'éléments volumiques en proposant différentes configurations de maillage.
Maillage grossier
La première itération a été réalisée avec un maillage très grossier, entraînant des besoins mémoire très faibles :
- Éléments : 24
- Nœuds : 110
- DDL : 330
- Stockage dense : 0,8 Mo
- Stockage creux : 0,1 Mo
Cependant, ce modèle était clairement inadapté à toute étude technique, tant du point de vue de la forme en plan (initialement ronde) que du détail des sections.
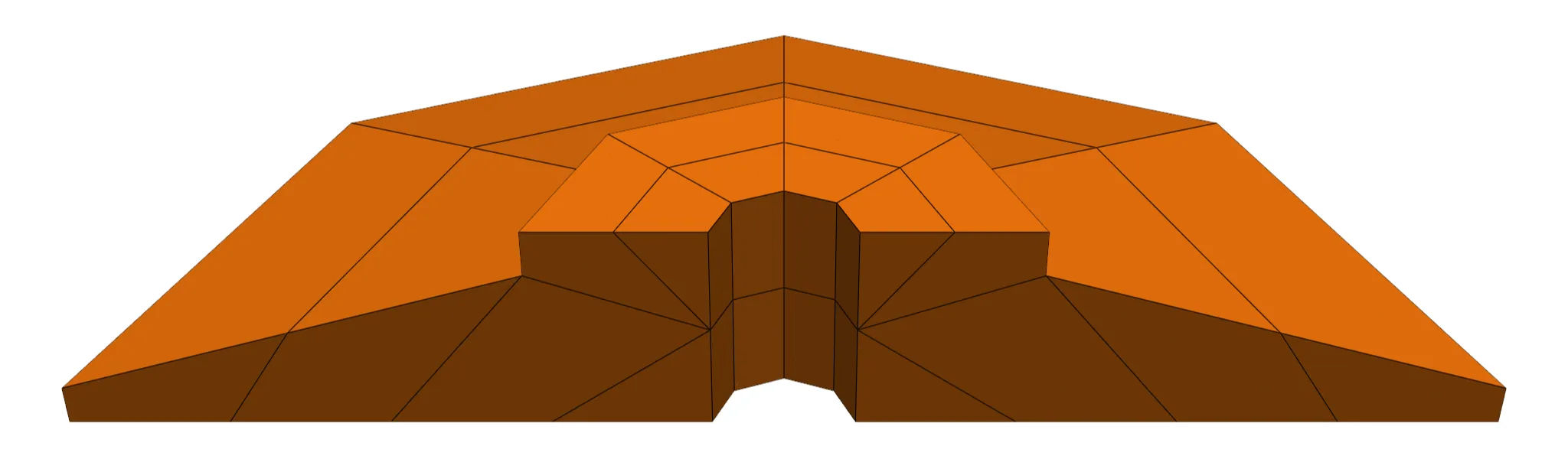
Maillage moyennement dense
En affinant le maillage, nous avons rapidement manqué de mémoire en utilisant un stockage dense de la matrice, comme le montre cet exemple :
- Éléments : 8k
- Nœuds : 35k
- DDL : 106k
- Stockage dense : 83,90 Go
- Stockage creux : 0,04 Go

Bien que le maillage puisse encore être affiné, ce modèle était déjà adapté aux analyses. Cependant, le stockage dense de la matrice était impossible sur notre ordinateur, tandis que le stockage creux restait parfaitement gérable.
Maillage dense
La dernière itération proposée utilisait un maillage beaucoup plus dense :
- Éléments : 66k
- Nœuds : 268k
- DDL : 803k
- Stockage dense : 4 801,8 Go
- Stockage creux : 0,3 Go

Pour ce modèle à maillage fin, le stockage dense était irréalisable même sur la plupart des stations de travail, nécessitant des ressources de niveau centre de données. En revanche, le stockage creux a réduit les besoins en mémoire de plusieurs ordres de grandeur, rendant le modèle (avec seulement 0,3 Go) facilement stockable même sur un smartphone d'entrée de gamme.
Résumé comparatif des maillages
Le tableau suivant présente un résumé de quelques-uns des maillages proposés pour l'étude de cette fondation d'éolienne :
| Éléments | Nœuds | DDL | Entrées non nulles | Dense [Go] | Creux [Go] |
|---|---|---|---|---|---|
| 24 | 110 | 330 | 9594 | 0.0008 | 0.0001 |
| 700 | 2,970 | 8,910 | 304,182 | 0.5915 | 0.0034 |
| 8,604 | 35,372 | 106,116 | 3,751,344 | 83.90 | 0.04 |
| 66,008 | 267,600 | 802,800 | 28,643,904 | 4,801.8 | 0.3 |
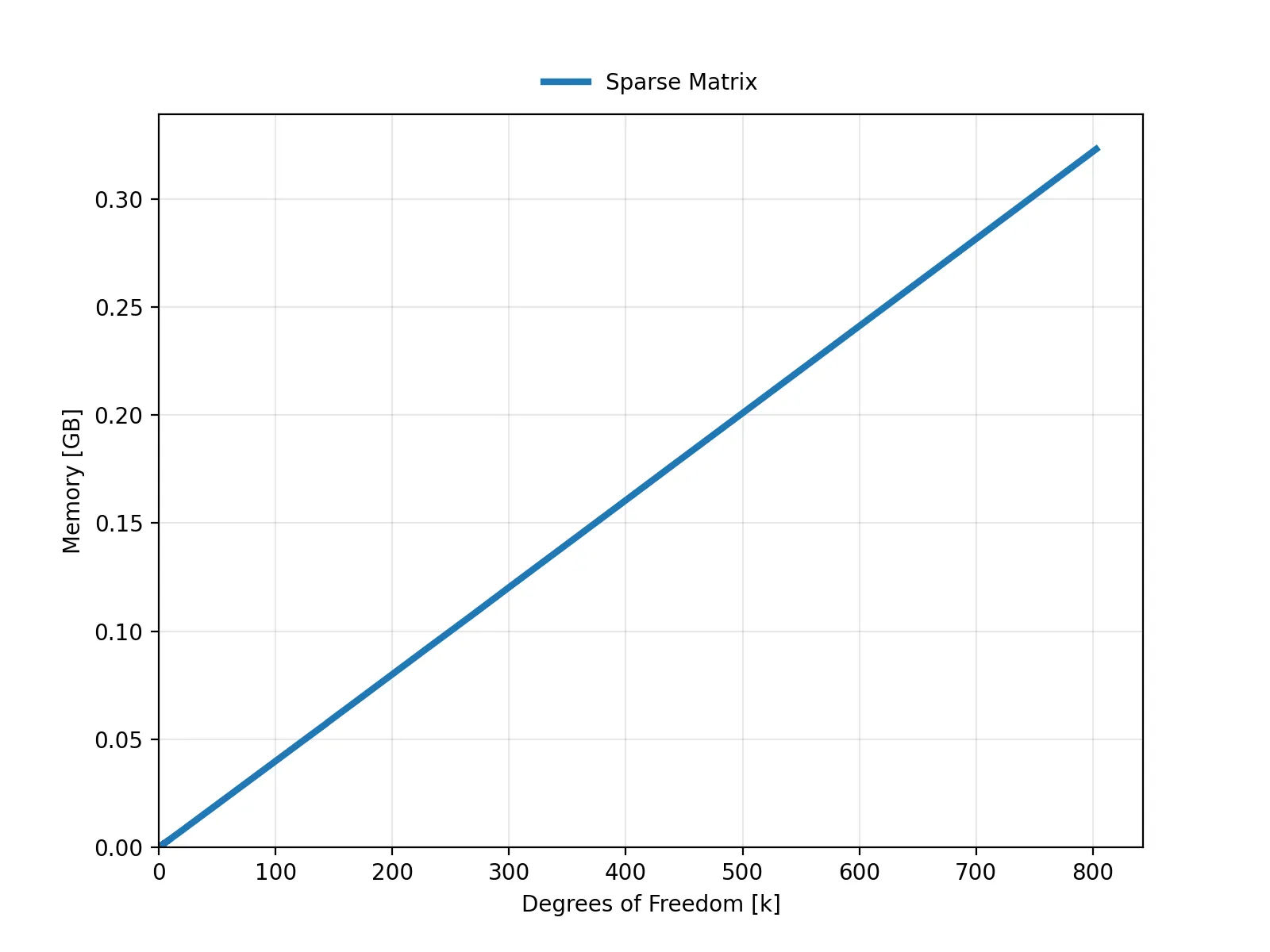
Cette vidéo montre l'évolution du nombre d'éléments et de l'utilisation mémoire pour les stockages dense et creux, ainsi que l'évolution du maillage de la fondation d'éolienne.
L'animation précédente illustre la croissance quadratique de la mémoire nécessaire au stockage dense, tandis que l'utilisation mémoire du stockage creux reste presque constante, quasi indiscernable de l'axe des abscisses. En isolant la dépendance de la mémoire creuse par rapport aux degrés de liberté, on constate que la relation est clairement linéaire.